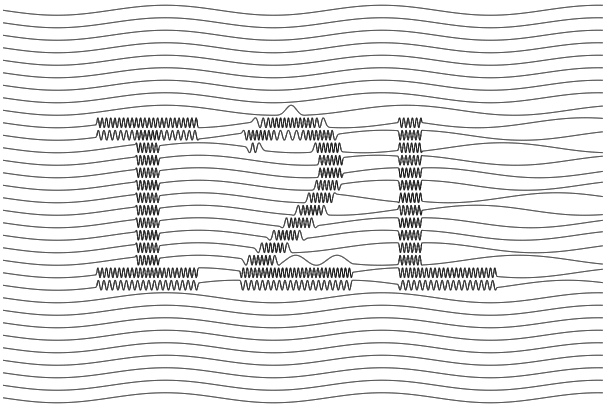
img2laser is a browser-based tool written entirely in Rust that can convert a bitmap image into a laser-ready SVG image using the sine wave line shading technique. In my original blog post, I showcased a Python notebook that performed the same task, but it was lacking in portability. I wanted to make the tool more […]
I started writing this post in 2018, shortly following a class I took on nanofabrication. The class focused on two methods of nanofabrication: e-beam lithography and DNA origami. I originally intended on writing a detailed introduction to DNA origami, but I don’t think I remember enough to do that now. Instead, I’ll briefly describe DNA […]
I am a huge fan of Mathematica for prototyping and quick one-offs. Most of the heavy lift analysis I do is with MATLAB or python, but sometimes I produce a graphic in Mathematica that I want to include in a publication. Here are a few tips on getting your Mathematica figures to look a little […]
Photoplethysmography (PPG) uses light to detect small changes in blood volume and is most commonly used for measuring heart rate. It is possible to buy a PPG-in-a-package that is smaller than a pinky nail. The MAX30101 comes in at just 5.6 mm x 3.3 mm and it doesn’t just measure heart rate — it does […]
My nephew’s birthday was coming up in a couple days and I wanted to build or (3D) print him something. He loves Hot Wheels, so I thought I’d make him a speedometer with a digital speed readout. I envisioned two LEDs illuminating two photoresistors. When the car speeds by it would block one photoresistor and […]
TL;DR: Convert a bitmap image into an SVG with sine wave line shading. See the code here: https://github.com/0not/laser_tools/ I recently built a laser engraver/cutter with a 30 W diode laser module and an OpenBuilds ACRO positioning system. I wanted a way to engrave moderately detailed images without having to deal with the slow speed of […]
In 2018 I posted a design of a simple spectroscope to Thingiverse. I figure I’ll re-post it here to try and reach a wider audience. This project was inspired by the Nanomaker course on MIT OpenCourseWare. Summary This project will teach you how to build a simple DIY spectroscope with an old CD, an empty […]